Lazily Computing the Singular Function of Bold Play

Suppose you are gambling at a casino where you can bet any amount $x$ between $0$ and $1$ dollars. If you win the bet (which happens with probability $p$ ) you get back the amount $x$ you had staked plus $x$ more. If you lose the bet you get nothing back.

We assume that you enter the casino with a positive wealth of less than a dollar. You consider the outing at the casino a success if you manage to come away with exactly $1$ dollar in total wealth. “Bold Play” is the strategy of betting your entire wealth whenever you current wealth is less that half a dollar and otherwise betting just enough that a win will make your wealth exactly one dollar. You walk away a success as soon as your wealth reaches a dollar and you are thrown out as a failure as soon as your wealth reaches zero.

It is a celebrated result that when $p<1/2$ Bold Play is an optimal strategy if your aim is to maximise your probability of success. But that is not our subject today. See Billingsely’s Probability and Measure and his article “The Singular Function of Bold Play” (American Scientist, 71(4), 392–397) for more of the story.

For a given value of $p \in [0,1]$ and $p \ne 1/2$ , the so-called “Singular Function of Bold Play” is the function on $[0,1]$ which gives the probability of success when starting Bold Play with wealth $x$ . If you consider $x$ as the state of the gambler and realize that in an ideal casino the past does not affect the future, you will see that this function is described by the relation: $F(x) = \begin{cases} 0 & x=0\\ 1 & x=1\\ pF(2x) & 0<x<1/2\\ p+(1-p)F(2x-1) & 1/2<x<1 \end{cases}$

For students of mathematical analysis this function is interesting because it is an example of a function arising out of a natural problem which is everywhere continuous and strictly increasing, possesses a derivative at “almost every’” point, and yet $F'(x)=0$ wherever the derivative exists.

The graph of $F(x)$ has a fractal character:

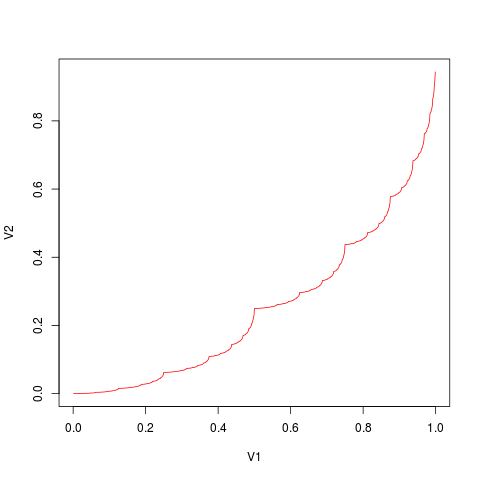
We present here a program in the programming language Haskell to calculate the value of this function on a grid of dyadic rationals (i.e. points of the form $k2^{-n}$ ).

Haskell is a language characterised by “lazy evaluation”: expressions are evaluated only when their values are needed. This allows us to define potentially infinite data structures in this language. A program definining such a data structure does not go into an endless loop as long as it is careful to use only a finite part of this infinite structure. This allows us to separate the production of an potentially infinite stream of data from the details of how much of it is to be consumed and how.

In our program we produce the values of $F(k2^{-n})$ for $0<k<2^n$ for $n=1,2,\ldots$ without end and then separately choose how many of these values to use depending on a command-line argument provided by the user.

This program also illustrates how the idioms of functional programming can be used to naturally express the recursive definition of a function like $F$ .

Imports

module Main where 
import Text.Printf (printf) 
import Control.Monad (forM_) 
import System.Environment (getArgs)

The data types

We represent the value $y=F(k/2^n)$ by constructor $FValue$ whose arguments are $(n,k,y)$ . This facilitates the iterative calculation. The function $toXY$ converts to the $(k2^{-n},y)$ representation. $depth$ is a simple helper function used later in choosing which of the computed values to keep.

data FValue = FValue !Int !Int !Double
              deriving Show

toXY::FValue -> (Double,Double)
toXY (FValue n k y) =  ((fromIntegral k)*(2.0 ^^ (-n)),y)

depth::FValue -> Int
depth (FValue n _ _) = n

Computing the values of $F$

The function $fvalues$ computes the values of $F$ given the probability parameter $p$ . This is the crux of the program. Note how $fvalues$ is defined in terms of itself, thus expressing the natural recursion in the definition of $F$ where value of $F(k2^{-n})$ allows us to calculate $F(k2^{-(n+1)})=pF(k2^{-n})$ and $F(1/2+k2^{-(n+1)})=p+(1-p)F(k2^{-n})$ .

To start off the calculation we provide the value $F(1/2) = p$ .

fvalues::Double->[FValue]
fvalues p = start:(concatMap next $ fvalues p)
            where 
              start = FValue 1 1 p
              next (FValue n k y) = [left,right] 
                where
                    left = FValue (n+1) k (p*y)
                    right = FValue (n+1) ((2^n) + k) (p+(1-p)*y)

The Driver

We want to invoke the command as singular n p where $p$ is the probability parameter and $n$ is the maximum value of $n$ for which $x$ values of the form $k2^{-n}$ are considered.

The program prints the $x$ and $F(x)$ values separated by tabs. Warning: a total of $2^n$ lines of output are printed, so be careful with your choice of $n$ .

parseArgs::[String] -> (Int,Double)
parseArgs (n:p:[]) = (read n,read p)
parseArgs _ = error "Usage: singular n p"

main::IO()
main = do
  args <- getArgs
  let (n,p) = parseArgs args
  let tuples = map toXY . takeWhile ((<= n) . depth) . fvalues $ p
  let printtuple(x,y) = printf "%g\t%g\n" x y
  forM_ tuples printtuple

Source Code

The full source of the program is available here.